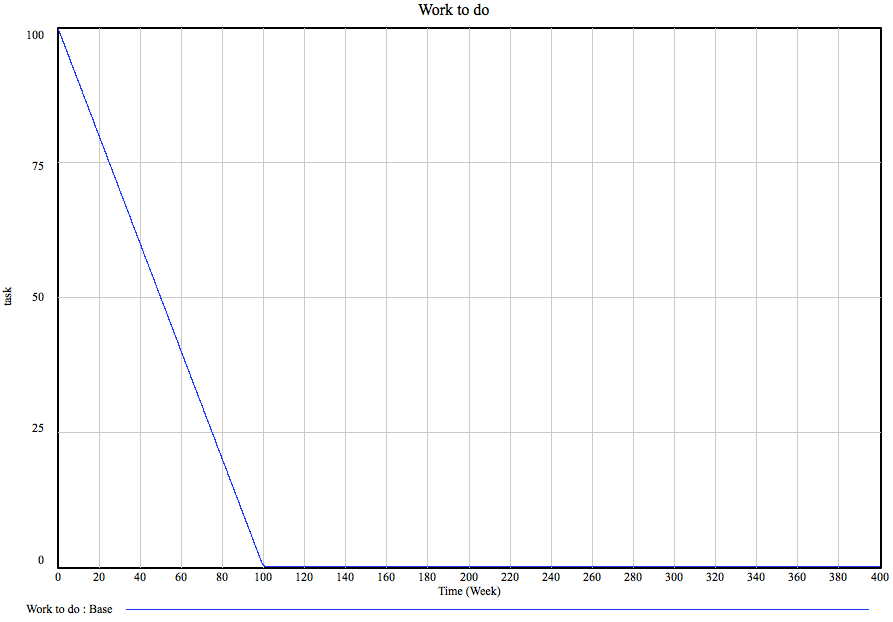
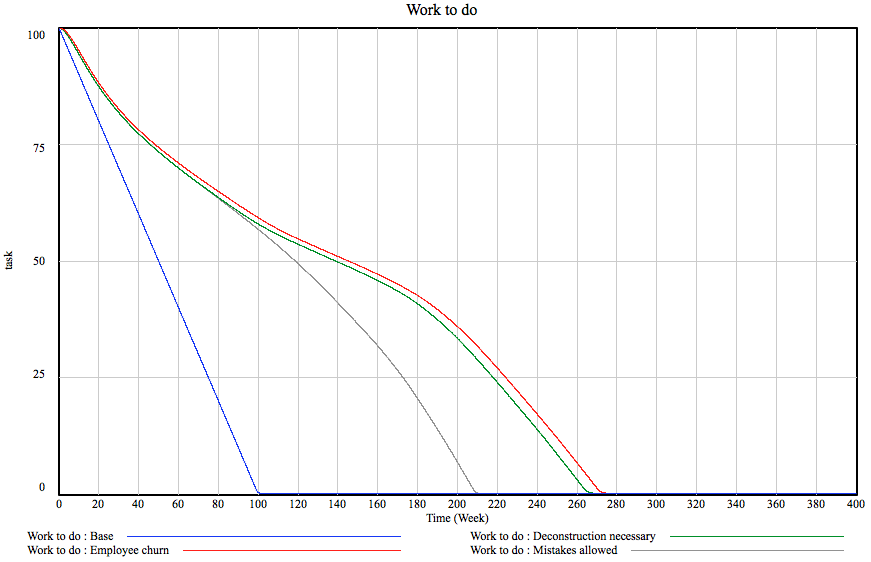
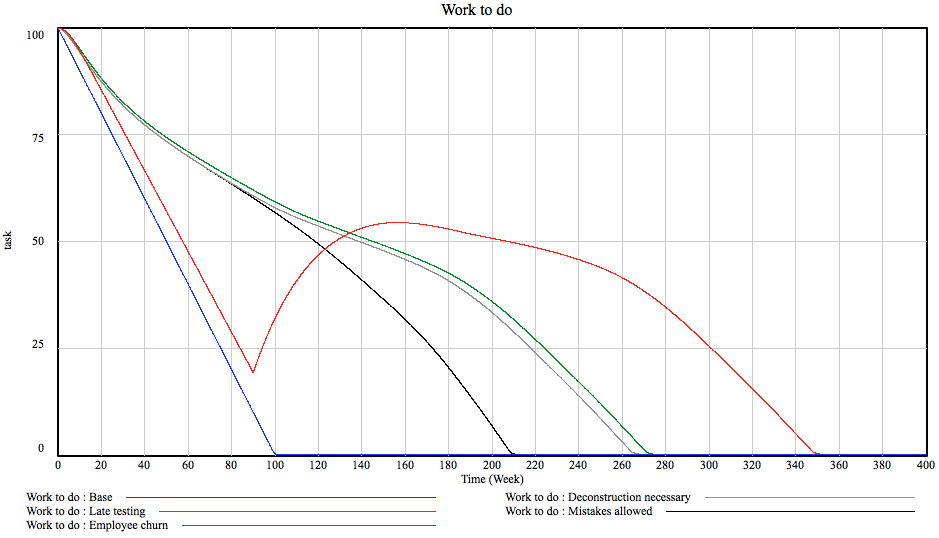
Oh dear, some horrible things happened around here with the gunman in the movies. For a second there I thought hey, this is a simple feedback loop between guns in the hands of criminals and guns in the hands of citizens, let’s make a post. Then I realized the magnitude of wrongness of me doing that. I also realized that the system is actually not that simple at all. Thus, we will continue with our regular programming delayed by a technical glitch and come back to the guns thing at a later time if at all.
Today we talk about traffic. Not least because this week professor Jay Forrester gave his lecture to the System Dynamics class. He is, of course, the grand old man of urban studies and last year at the same class he said something really interesting (am quoting from memory) about the topic: “Whenever you decide to make something better, you are just pushing bottlenecks around. You need to decide, what you are willing to make _worse_ in order to achieve a lasting result”
I have lately made the mistake of following up on Estonian media and, based on the coverage, one of the most pressing issues there is that the city of Tallinn has overnight and without much warning halved the throughput of certain key streets.
While we speak, the Euro is falling, US is in the middle of a presidential debate, the Arab world is in flames, we are on a verge of a paradigm shift in science, Japan is making a huge change in their energy policy possibly triggering a global shift and all of this is surrounded by general climate change and running out of oil business.
Oh, well. We probably all deserve our parents, children, rulers and journalists.
Anyway, that piece of news seemed to match perfectly the words of Jay Forrester and thus todays topic.
What the quote above means is that tweaking system values will just prompt more tweaking. Making a road wider will encourage more people to drive on it necessitating expansion of source and sink roads which have source and sink roads of their own. Thus, what professor Forrester says is that in order for that cycle to stop, one must make a conscious decision _not_ to improve certain things. Yes, traffic is horrible but instead of adding more roads, what else can we do? How can we change the structure of the system rather than tweaking and re-tweaking certain values that will only result our target variable stabilize at a (hopefully more beneficial) level?
This brings us back to Tallinn. From one hand it might seem that the change is in the right direction: somebody has decided to make the lives of drivers worse in order to stop pushing the bottlenecks around.
Applause!
Or maybe not. You see, what Jay Forrester definitely did not mean was that _any_ action resulting in somebody being worse off is beneficial for the system. Only careful analysis can reveal what change can overcome the policy resistance of a given system.
The following is based on public statements about the future of public transport in Tallinn as reflected by media. It would certainly be better to base them on some strategy or vision document but alas, there is none. At least to my knowledge and not in public domain. There was a draft available on the internet for comments last summer but that’s it.
Uhoh.
Let’s see, then. When driving restrictions are applied, two things happen. Firstly, amount of people driving will go down simply because it is inconvenient but also, the _desire_ to go downtown will diminish after a while. I’ll go to the local shop instead of driving. Let’s lease our new office space somewhere with good access rather than downtown. That sort of thing. When willingness to drive downtown diminishes, amount of people driving certainly goes down but so will the number of people taking the bus: if the need and desire are gone, there is no point in standing in the bus stop, is there?
It has been publicly stated that the money acquired from making the lives of drivers harder (this includes high parking fees, among other things) will be used to fund adding capacity to public transport. Therefore, the less people drive, the less money there is to maintain some headroom in terms of capacity. The less headroom we have the higher the chance that the person taking the bus does not want to repeat the experience and prefers not to the next time. And, of course, investment in the road network drives up the amount of people who actually drive.
Simple, isn’t it? Before I forget, many of these causal relationships have delays. Offices do not get moved and shops built overnight, investments take time to show results. It takes time for people to realize they don’t actually want to spend 2 hours each day in traffic.
Here’s a diagram of the system I described.
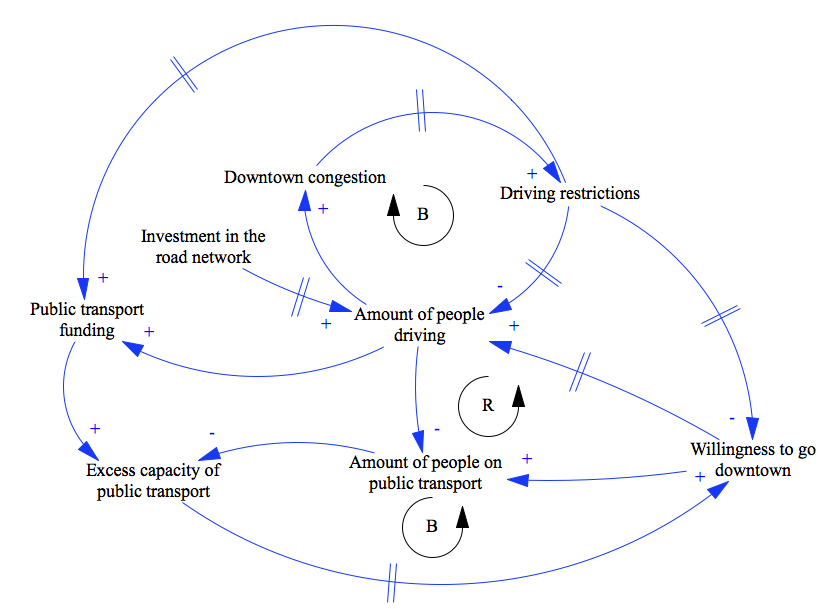
Now, tell me, what changes in what variables and when will result in sudden and rapid increase in driving restrictions that occur simultaneously to a massive investment to road infrastructure at city boundary?
Nope, I have no idea either. From the structural standpoint, the system is a reinforcing loop surrounded by numerous balancing loops. Since several of them involve delays, it is very hard to tell whether the system would stabilize and when. It seems though that in any case, a reinforcing loop driving down the willingness of people to go downtown gets triggered. The danger with these things is, of course, that when they _don’t_ stabilize or stabilize at a lower level than desired, downtown will be deserted and left only to tourists (if any) as the need to go there diminishes. The citizens not being in downtown kind of defies the point of making that downtown a more pleasurable place, doesn’t it?
Surprisingly, the city of Tallinn has actually done some things to break the loops described. For example, the public transport system has operated on non-economic principles for years and years. The city just pays for any losses and there is no incentive to make a profit. This makes the system simpler and removes a couple of fast-moving economic feedback loops. For this particular campaign, however, taxation on drivers was specifically announced as a funding source for public transportation without much further explanation.
The system is an interesting one and had I some numbers to go on, would be fun to simulate. But I think I have made my point here. Urban transportation is a problem of high dynamic complexity. When the system described above was to be cast into differential equations, there would unlikely to be an analytical solution. How many of you can more or less correctly guess a solution to a Nth order system of partial differential equation? Without actually having the equations in front of you? Do it numerically? Right.
It is thus imperative that decisions that could easily result in rather severe consequences to the city are based on some science or are at least synchronized amongst each other (did I mention it? There is a multi hundred million euro development project underway to radically increase the capacity of a certain traffic hotspot in Tallinn) using some sort of common roadmap.
I hope this excursion into local municipal politics still provided some thoughts on system dynamics in general and hope you’ll enjoy some of it in action over a safe weekend!