SD Action!

Since the previous post got a lot of good feedback and a ton of comments. Let’s follow up.

The question is, why is G+ flopping? I mean, its like a desert, Steve Yegge’s rant is the only piece of content I’ve ever found there. And even that was referred to from somewhere else.

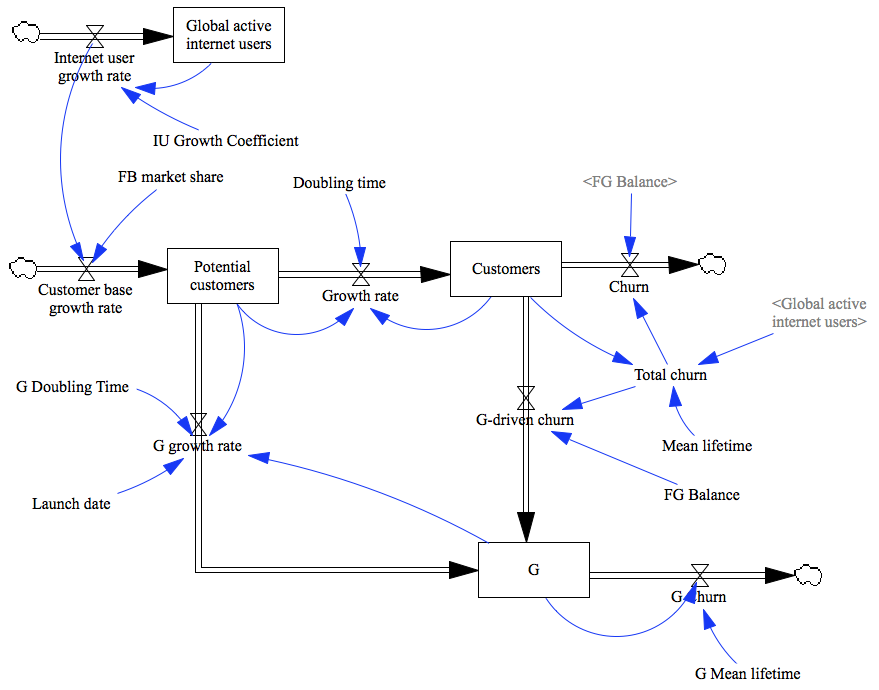
In a wider context the question is, what would it take for something brand new to take on Facebook and significantly alter the behavior depicted previously. To answer this, I amended the model:

As you can see, it is now considerably more complex. There is now a new box ingeniously labelled “G” and a flow from potential users that fills it. By doing this, an assumption is introduced that the potential customers of Facebook and the new service will overalp. There is also a flow from “Customers” to “G” and considerable changes in how churn is calculated. Previously, as you might remember, churn was just a function of how many users Facebook has and depended on the average lifetime of active users (whatever the definition of an “active user” is). This is slightly unrealistic: the less users facebook has, the less reason for people to be there as the chances of majority of their friends not being active goes up. So I fixed that. Total churn is now calculated like so:

Customers/(Mean lifetime*(Customers/(Global active internet users))^0.07)

The “0.07” effectively determines how fast the function approaches 1, i.e. how much impact the outside world has on churn. A new variable “FG Balance” determines, what percentage of the people leaving Facebook would become active users of the new service.

Let’s now take a look at how these changes affect what we can say about the future of Facebook. Let’s start simple and just assume that the new service is after the same user base but that the existing Facebook users are extremely loyal and there is no leakage, this shall be our scenario “G”. The G doubling time parameters are set to match what is known of G user base, mean life-time is the same as for FB and the service is set to launch on day 2692 of Facebook Reckoning with 2.5e+07 users. The reason for this is that the behavior of the networks is very different in the beginning and at scale simply because their target community changes so much. Remember how Facebook conquered one small college market after another (why this matters, is a small thinking exercise for you, my dear reader)? Remember the rush to get early G invites? Anyway, here we go:

Yup, there is no way the new service will catch up with Facebook like this. Even when we make the new service virtually explode by making it grow three times as fast as the figures suggest (scenario “Super_G”), it will not overtake Facebook before 2015. The reason for this is simple: scale is king here. The more users you have, the more you attract. Thus, tapping potential customers is not enough, G needs to attract FB users. Let’s see what happens if a third of people leaving FB would join G:

Oh my. Even for that rather generous case, the blue line crosses the red one in about five years… In both cases, it is interesting to note te effect on Facebook: for both scenario its fundamental growth pattern does not change. It will flatline a while longer or loose some customers for a while but it will eventually continue to grow and grow fast.

This is not looking very promising, is it? Let’s dial everything to pretty much eleven and picture a scenario where two thirds of all people leaving FB would join G and that the competing service is so attractive that the average half-life of FB users drops 30% (Scenario “G_Super_Pull”):

This is much more interesting. FB general behavior does not change but G growth takes a sharp turn up as soon as FB churn peaks. Which is right about now, more or less. Ergo, a similar scenario might be happening and we don’t know it yet. That said, the input parameters are pretty outrageous and very unlikely to be true and the FB should have less users now already. Still, it is curious to think that G might be about to overtake Facebook and nobody knows it yet. Interestingly, changing the percentage of Facebook churns converting to G has less of an impact than the overall increased churn of Facebook.

Interestingly, the fundamental modus operandi of Facebook will not change: some scenario prolong the flatline phase and some induce a small decline but all the lines point up. Playing with the “effect of the outer world” constant has little impact as well.

The main conclusion I can draw from this exercise is that Google needs to actively target Facebook users, convert active facebookers who are happy with the service to active G+ users to have even a remote chance of making a dent in their armor. Rapid user acquisition would not do, only conversion. And the conversion rates must be very high indeed.

The second, and more important conclusion seems to be that one needs to mess up royally to loose in the social network game. The amount of people joining the interweb is so large that even with massive churn and people quitting in favor of your competitors, there is still a huge crowd of people to recruit. Which is something I would not have thought.

As we are done now with the analysis part, it is probably appropriate to point out that this model has an important flaw. It assumes that Facebook and Google define active users similarly. This is unlikely to be true: Google calls even their reader app part of G+ so God knows what their numbers might actually mean. It was also pointed out that there is actually little churn in social networks, you just don’t stop by as often as you used to but you never churn. And there is the question, how can we use such insights to predict future growth.

But, yet again, the ink in my pen has dried and the answers need to wait until next time. See you around!

I had an argument. Not that this is peculiar per se but I had an argument about Facebook. On Facebook. It was about FB buying Instagram for $1B and I told a friend that “Facebook will peak, trust me”. I never thought to doubt this assumption as I figured that eventually the supply of potential customers would run out, churn would take over and it would be downhill from there as the less users there are the less reason it is for others to be there.

I was wrong. I should have known, really. Its a shame I didn’t. Stuart Fierstein once said “There is no surer way to screw up an experiment than to be certain of its outcome”. All of the system dynamic education teaches you that humans can’t predict behavior of dynamic systems.

Oh well.

Anyhow, I decided to run the numbers and so I did. Using Vensim, I built the following model:

Let’s walk through it. First thing to consider is that FB does not operate in a vacuum or a world of infinite users. They can only reach people who actively use internet. That’s the box “Global active internet users”. Based on Google Public Data (which is awesome, by the way) one can extrapolate that this number multiplies by roughly 1.00037437 every single day (that’s the “IU Growth Coefficient”). It can be assumed that a certain percentage of the people adding to the global internet community will be potential FB customers but not all: not everybody speaks a language FB is available in, not everybody likes FB or has time for it. I assumed that 80% of people (the “FB market share variable”) would, indeed consider becoming a FB customers. Thus the FB potential customer base (labeled as such) grows by a number that is called “Customer base growth rate” on the model.

However, not all of these people instantly become FB users. It is merely a base from which FB can recruit new ones. The speed at which this happens is dependent on three factors. Firstly, the doubling time (i.e. the time during which as much people would become customers as there already are). This is measured in days and I used 250 for the simulations. Secondly, the user base growth rate depends on the number of customers FB already has for a simple reasons: the more users there are the bigger their joint community of friends that might join FB. However, this effect is countered by the third factor, the potential customer base. The thing is that the smaller the community from which the customers could come from, the higher the chance that the friend networks of individual users overlap. Simply put, if FB had 10 users, these users would have about 400-500 friends and 1000 users would have ten times more. But if there was just 1000 users left who are yet to join FB, they’d be bound to be connected to _somebody_ already there. Clear? Didn’t think so. Think about it and it starts making sense, though. If not, there might very well be an error of reasoning in which case please be so kind to leave a comment.

Alright. But there is also churn. In order to keep things simple, churn is signified by mean tenure of a user, is represented in days and is 1095 days or three years in our case.

Finally, there is the issue of time. In our simulation, day 0 is the day of Facebook launch and all models start from when there is the first available user count: FB had 100 000 000 users as of 4th of February 2004. This means that today is the day #2949 of Facebook Reckoning.

And that’s our model. Of course its a very simple one and does not accurately depict a large number of factors impacting the growth of a social network and it makes a large number of assumptions (that churned users never return, for example). It does however match FB growth numbers pretty accurately and it is hard to see fundamental fault in the logic presented above. If you can spot one – do let me know. That’s the beauty of SD analysis: you don’t have to be right on money with your numbers, you want to have the relationships roughly accurate instead. You’ll be after general behavior rather than an exact user count at a given time.

So I ran the model. The result? Here:

The line to watch is the blue one. It is obvious that it does not peak. In fact, it flattens out right about now (how about that?) and stays flat for about two years before climbing again. The reason for this is not so obvious. If you look at the blue and grey lines (FB users and global internet users respectively) you can see that they move about parallel for a while. The red line (potential customers) of course goes down as more and more people join FB and not enough people join the Internet community. At about day 2635, FB join rate peaks before starting to fall as there are simply not enough people who use internet but have not used Facebook. And so there is a decline in growth rates up to about day 3300 where the black and green lines cross. What does this means? Simply that at that point the Internet grows faster than Facebook. Hence, the potential user base starts increasing again and Facebook adoption starts slowly climbing up.

Pretty neat, huh? Besides being exceedingly cool in my geeky mind, all this has following very real business consequences.

• Don’t panic! Yes, your growth will be flat for a while but this is not because you are doing something wrong, it is because you have outgrown the Internet. Keep cool, calm down and it will be allright. The biggest danger here is that flatlining AU numbers mean flatlining revenue numbers and that spells trouble. A temptation is created to drive up ARPU which results in stronger advertising pressure which is likely to drive away users, slow growth even further (remember the friend-of-friend concept of growth) and ultimately start a death spiral (the less users the less reason for others to be there)
• Recruiting new users is actually dangerous, you are better off making sure they don’t churn. The following chart tells the story. The green line is the user count for our base case, red line shows the case with mean user lifetime increased by 30% and the blue one the case where adoption rate was similarly increased. The trouble with increasing adoption is that it just makes you spend you user base faster and increase the time it takes for the Internet to catch up with you. Focus on keeping your existing customers instead and the increase can be substantial

Of course a disclaimer goes with all this. All models are wrong but some models are useful. Into which bucket this particular model falls is up to you, my dear reader but this is simply a couple of lines and boxes on a computer screen and not the huge business Facebook has become. So no fingerpointing should I turn out to be wrong, OK?

Finally, I’d like to say that there is a ton of interesting things these sorts of models can explain. For example, I’m pretty sure G+ being a slosh has a simple reason related to SD, it would be cool to simulate increase in advertising pressure and so on and so forth but let’s leave it all for some other time, shall we?